Inkluderende matematikkundervsining
På denne siden finner du prinsipper for inkludering, beskrivelse av virkemidler som kan benyttes og forslag til inkluderende, elevaktive undervisningsopplegg.
Skolen skal være inkluderende. Det slås fast både i opplæringsloven og i læreplanens overordnede del, der det understrekes at elever lærer i samspill med andre, gjennom kommunikasjon og felles læringsprosesser. Likevel viser forskning at elever med sansetap ofte får mye én-til-én-undervisning.
Å inkludere en elev uten syn i klassens matematikkundervisning, krever at oppleggene planlegges slik at innholdet kan erfares gjennom andre sanser enn synet – for eksempel gjennom taktile modeller, lyd og kroppslig aktivitet, istedenfor å tilpasse til punktskriftbrukeren etter at økten er ferdig planlagt. Denne typen undervisning styrker ikke bare læringsutbyttet for eleven som er blind – den kan også gi medelevene økt forståelse, variasjon og bedre begrepslæring.
Matematikk læres ved å reflektere over erfaring gjennom opplevelser og sanseinntrykk. Mange begreper utvikles spontant hos seende barn gjennom hyppige og kontinuerlige visuelle inntrykk. Elever som er blinde må få tilsvarende erfaringer gjennom å kjenne, bevege seg, lytte og samtale.
Det kan kreve litt ekstra tid til planlegging i begynnelsen. Det beste er om klassens lærer og ITO-læreren samarbeider. En måte å organisere dette på og samtidig ivareta eleven som bruker punktskrift kan være å bruke to-lærer-system i faget. Målet er at den blinde eleven kan være en aktiv deltaker i læringsfellesskapet.
Virkemidler som erstatter synsinntrykk
- Konkreter i matematikk kan være med på å gjøre figurer og illustrasjoner mer tilgjengelig for elever med nedsatt syn.
- Konkreter kan benyttes til å øke forståelsen av begreper ved å gi variasjon og mulighet for utforskning av begrepene.
- Konkreter og taktile illustrasjoner kan benyttes i samarbeid og kommunikasjon for alle elever.
- Aktiviteter med bruk av kroppen, kan gjøre det lettere å huske og forstå innhold i begreper. Kan gi en praktisk erfaring som man kan bygge videre på.
- Lydillustrasjoner gir en ekstra dimensjon og opplevelse som kilde til relasjonell forståelse for alle elever.
- Les mer om taktile illustrasjoner figurer her (Lenke kommer).
Når eleven ikke følger klassens progresjon
Når punktskriftbrukeren har andre læringsmål enn de andre i sin klasse, anbefaler Statped at hele klassen likevel arbeider med samme tema. Mange praktiske matematikkoppgaver med utforsking og samarbeid kan gjøres sammen selv om ulike elever har ulike læringsmål for økta. Eventuelle refleksjonsspørsmål og skriftlige oppgaver som hører til, kan tilpasses etter ferdigheter. Når avstanden føles stor kan det være nødvendig å ha en-til-en undervisning i matematikk, men dette bør være unntaksvis.
Opplæring i kompenserende ferdigheter knyttet til matematikkfaget (for eksempel Kalkulatorløsninger, tolking av taktile illustrasjoner, navigering i tabeller og lignende) bør flyttes til ressurstimer utenfor matematikktimene slik at eleven får like mye tid som de andre elevene på å arbeide direkte med kompetansemål i faget. Eleven har rett på ekstra undervisning etter opplæringslovens §3-5/6-4 og §11-5.
Forslag til inkluderende, elevaktive undervisningsopplegg
Mål: Eleven skal få mer erfaring med å tolke og sammenligne brøk, ved å lese verdien av brøk i spill
Tidsbruk: ca. 30 min
Foreberedelse: Gjøre klart utstyr; Du trenger spillkort med punktskrift. Dette fås kjøpt i flere nettbutikker og kan lages selv.
Gjennomføring:
Elevene spiller to og to med en kortstokk uten billedkortene.
Begge spillere trekker samtidig to kort. Begge spillere skal så lage hver sin brøk med kortene ved å legge det med lavest verdi som teller og det med høyest verdi som nevner (ekte brøk). Den med høyest verdi på sin brøk, vinner stikket. Spillet fortsetter til en har vunnet alle kortene.
Mål: Eleven skal få introduksjon i og erfaring med begrepet variabel.
Tidsbruk: ca. 60 min
Forberedelse: Eleven som ikke ser bør få informasjon om oppstarten på forhånd, ettersom læreren viser frem konseptet med aktiviteten ved oppstart. Du må vurdere om eleven skal få informasjonen som skrives på tavla ved oppstart, i et dokument på PC slik at eleven kan følge med på leselista si.
Lag klar noen algebraiske uttrykk med s (skritt), h (hopp) og f (fot/museskritt).
Gjennomføring:
Lærer stiller seg ved en vegg og ber elevene følge med. Læreren går tre skritt tar to hopp og går to museskritt. Samtidig som han forklarer; «frem, frem, frem – hopp, hopp – fot, fot.»
Spørsmål til elevene: Hva gjorde jeg nå? Elevene beskriver.
Spørsmål til elevene: Hvor langt kom jeg fra veggen? Elevene diskuterer/beskriver.
Lærer skriver opp på tavlen det som ble gjort:
3 skritt +2 hopp +2 fot
Spørsmål til elevene: Hvis jeg nå tar 2 skritt, 1 hopp og 4 fot, vil jeg komme kortere eller lengre fra veggen en forrige gang?
Elevene får prøve ut i samhandling.
Diskuter/kommenter resultatet. Spørsmål til elevene: Kunne læreren jukset?
Skriv opp på tavlen, med forkortelser, det som ble gjort:
2s +1h +4f. La elevene si hva bokstavene står for.
Lærer skriver ned fire uttrykk som elevene skal skrive ned i boken sin og så gå etterpå.
Eksempler:
- 5s +4s +5h +3f
- 5h +3s +6f -2h
Spørsmål til elevene: Hva tror dere må skje når det står minus? (hoppe baklengs)
- 6s -2h +9f -3f +12h +7s
- 10s +3f +10 h+2s +15h -7s +10f -25h
Klassen får utforske utendørs:
Hele klassen går ut og stiller seg langs en vegg/linje så går de nr. 1. De må stoppe der de kommer. Elevene kan ha med seg uttrykkene på papir. Medelevene må lese opp for hverandre, eller så må lærer lese de høyt for at punktskriftsbrukeren skal ha uttrykket.
Spørsmål til klassen: Hvorfor kommer ikke alle like langt?
Hvis tid får elevene samarbeide to og to eller tre og tre der hver elev lager en oppgave som de andre på gruppen skal gå.
Klassen går inn i klasserommet.
Lærer setter = etter oppgavene som fremdeles står på tavlen og trekker sammen.
Spørsmål til klassen: Hvor mange hopp hadde dere trengt å ta i oppgave 4?
Oppsummering: Drøfte hva bokstavene står for og hvordan en størrelse kan variere: Introdusere begrepet variabel.
Mål: Eleven skal få erfaring med begrepene figurtall (kvadrattall).
Tidsbruk: ca. 45 min
Forberedelse: Gjøre klart utstyr; små klosser eller tellebrikker. Vurdere hvordan parene skal settes sammen. Punktskriftbrukeren kan med fordel få erfaring med brikkene på forhånd.
Gjennomføring:
Elevene arbeider sammen i par og skal lage kvadratiske figurer (kvadrattall) sammensatt av brikker/klosser.
Oppgave: Lag kvadratetene 1*1, 2*2, 3*3… med klosser/tellebrikker.
Sett opp et regnestykke og finn ut hvor mange brikker du trenger for å lage den 6. figuren. Forklar hvorfor det blir sånn og bygg det.
Drøfting i parene:
Trenger dere å bygge den 10. eller 100. figuren for å finne ut hvor mange brikker de inneholder?
Hva med kvadrat nr. n? Hvorfor blir det sånn?
Videre arbeid: Samme fremgangsmåte med ulike figurtall. Drøft økning og generell formel for figur nr. n.
Variasjon: Paret legger resultatet frem muntlig for lærer eller levere inn skriftlig utregning og forklaring.
Mål: Eleven utforsker begrepet faktorisering.
Tidsbruk: ca. 30 min
Forberedelse: Gjøre klart utstyr; klosser. Eleven uten syn kan få et sorteringsbrett for å holde oversikt over klossene. Om dette er nødvendig varierer. Eventuelt vurdere gruppesammensetning.
Gjennomføring:
Elevene får utdelt klosser, de arbeider to og to.
Oppgave: Ta 24 klosser og del de i like store grupper. Drøfting: På hvilke måter kan dere gruppere 24? Skriv ned svarene deres.
Variant: Del klassen i 2. 12 elever skal stille seg opp i grupper med like mange personer på hver gruppe. Hvor mange måter kan dere gjøre det på?
Drøfting/diskusjon: Kan vi lage regnestykker av dette? Hvordan ville dere satt de opp? Hva betyr faktorisering?
Videre arbeid: Ha brikker tilgjengelig når elevene arbeider med faktorisering. Faktoriser større tall.
Mål: Eleven skal øve på praktisk bruk av brøk og prosent.
Tidsbruk: ca. 45 – 60 min
Forberedelse: Gjøre klart utstyr; Kvadratiske brikker med ulik tekstur. Om man har brikker på skolen med ulik farge kan man feste på punktskrift eller annet for å skille dem. Det bør være mange brikker, da noen elever vil komme til å bruke prosenttall som antall. Forbered forholdstallene. Hvor stor andel av åkeren skal være rug osv.
Gjennomføring:
Elevene får ut brikker/klosser i fire forskjellige farger. Elevene jobber i grupper på 4. De skal lage en åker der det er en gitt fordeling mellom kornsortene. Hver kornsort har sin farge. De 4 opplysningene om hvor stor del hver kornsort har av hele åkeren ligger i hvert av de 4 hjørnene i klasserommet. F.eks; Hvete (Rød) skal være 35%, Rug (grønn) Skal være 1/5 osv. Hver elev har ansvar for at den opplysningen de har funnet stemmer i den ferdige figuren.
Tilrettelegging: Hvis brikker/klosser har lik struktur, kan det være nødvendig med synstolkning i forhold til fargene.
Utvid: Elevene kan bruker så mange klosser de vil. Hvis de bruker 100, stemmer prosenten direkte og de kan bli utfordret til å lage åkeren halvparten så stor osv.
Mål: Eleven tilegner seg praktisk erfaring med måling av lengde
Tidsbruk: ca. 45 min
Ute hvis mulig. Eleven jobber i grupper på tre. De får utdelt ett tau/en tråd. Oppgave: de skal lage en knute for eksempel 2,65 m inne på tauet. De har ingen hjelpemidler utenom seg selv og omgivelsene. Hvem kommer nærmest? Hvordan tenkte de? Hvilken strategi brukte de?
Variasjon: Hvis ingen er helt i mål kan gruppene prøve-måle etter en stund.
Mål: Innføring i egenskapene til et koordinatsystem
Tidsbruk: fra 20 min
Forberedelse: Koordinatsystem kan også arbeides med i punktskriftstimen til den blinde eleven. Vi anbefaler en trinnvis tilnærming.
Gjøre klart utstyr; Geobrett (strikkbrett). Det kan være en fordel med kraftige strikk.
Gjennomføring:
Elevene jobber to og to med et Geobrett (strikkbrett).
Oppgave: Lag ett koordinatsystem med en x- og en y-akse.
Diskusjon/drøfting: Hvorfor laget dere det sånn? Hvordan kan det gjøres på en annen måte?
Arbeid videre: Kan dere flytte origo? Prøv å få en, to og fire kvadranter. Tilføre punkter.
Mål: Eleven skal få kjennskap til lineære funksjoner.
Elevene får utdelt strikkbrett med x- og y-akse, og graf fra origo og til et gitt punkt med strikk.
Oppgave: Finn funksjonsuttrykket. Lag en ny graf som din medelev skal finne funksjonsuttrykket for. Bytt.
Refleksjon: Hvordan fant dere uttrykket?
Tilrettelegging: Kraftig strikk og strikk i kontrastfarger.
Mål: Utforske egenskaper til ulike geometriske figurer
Tidsbruk: ca. 30 min
Elevene får utdelt strikkbrett to og to. De deler brettet inn i 9 ruter ved hjelp av strikk. Oppgave: Lag så mange ulike trekanter du kan (en i hvert rom).
Drøfting: Hvorfor er de ulike? Kan de ha samme form, samme størrelse? (trekke inn begreper; formlikhet, kongruens)
Kan dere navnet på noen av trekantene?
Oppgaven kan gjøres likt for firkanter.
Opplegget kan utvides med mange ulike tall for areal og omkrets. Greit for repetisjon av begrepene og bygge forståelse av hva de betyr.
Mål: Praktisk erfaring med begrepene omkrets og areal
Tidsbruk: ca. 30 min
Elevene samarbeider to og to og får ut strikkbrett. Tallene i oppgavene er eksempler, her man velge flere ulike tall.
Oppgave: Lag en firkant med omkrets 24. Kan dere lage ulike firkanter?
Oppsummere i klassen. Hvilke løsninger fikk de? Hvorfor?
Lage en firkant med areal 16. Kan dere lage ulike firkanter?
Oppsummere i klassen. Hvilke løsninger fikk de? Hvorfor?
Opplegget kan utvides med mange ulike tall for areal og omkrets. Greit for repetisjon av begrepene og bygge forståelse av hva de betyr.
Tilrettelegging: Kraftig strikk og stikk i kontrastfarger.
Mål: Praktisk bruk av formler for volum
Tidsbruk: ca. 60 min
Forberedelse: Ta med ulike gjenstander som gryte, boks, ulike 3-figurer som kan fylles med vann, med ulik grunnflate. Det være lurt at den blinde eleven får gjøre seg kjent med de ulike gjenstandene på forhånd slik at de vet hva de kan velge.
Gjennomføring:
Elevene samarbeider i par og velger en gjenstand de skal finne volumet av. De må regne det om til dl før de får et litermål og tømmer oppi akkurat det volumet de har regnet ut. Hvis det er for mye og de søler, må de tørke opp.
Tips: lurt å veilede elevene i ut ifra vanskegrad. Ulike grunnflater gir ulike utregninger.
Mål: Få erfaring med begrepene målestokk, areal og måleenheter
Tidsbruk: fra 45 min
Forberedelse: Plantegninger med mål må være klar til timen. Både visuelt og taktilt. Plantegninger kan lages på tegneplast eller med punktskriver/svellmaskin.
Gjennomføring:
Lag/jobb med en plantegning av hus for å finne areal og lengder (omkrets) i de ulike rommene og hele grunnflaten. Bruksareal og bruttoareal og så bruke dette videre til å regne ut hvor mye det vil koste å male, legge fliser eller å legge gulv med priser hentet fra ulike leverandører.
Tilrettelegging: Her kan plantegningen lages på tegneplast eller svell-papir for å få den taktil.
Merk: Dette kan godt være et tverrfaglig opplegg sammen med kunst og håndverk.
Videre arbeid: Lage en modell av huset i papp med overflater malt/dekket og innrede med møbler.
Mål: Få praktisk erfaring med sammenhengen mellom diameter og omkrets av sirkel
Tidsbruk: ca. 30 min
Elevene arbeider i par. Elevene tegner en sirkel. Den må tegnes ordentlig og være stor nok til at man kan utforske den med tråd.
Videre klipper elevene et stykke tråd som er diameteren lang.
Elevene prøver ut.
Hvor mange slike lengder trenger man for å dekke omkretsen av sirkelen?
Blir det slik hos alle parenes sirkel?
Knyttet opp mot denne erfaringen kan man innføre formel for omkrets av sirkel.
Mål: Bygge klassemiljø
Opplegget forutsetter at klassen har fått en innføring av tallet pi.
Hele klassen skal f.eks. kunne de 100 første desimalene i pi. Med 25 elever i klassen kan det fordeles slik at de skal huske 4 hver. (her har antall elever i klassen litt å si) La gjerne elevene organisere selv. F.eks. kan elevrådsrepresentanten få ansvar for organiseringen.
Klassen får en frist og skal stille opp og si desimalene i riktig rekkefølge.
Gi gjerne en ny mulighet hvis det ikke går første gang. Denne fellesutfordringen kan godt resultere i belønning/hyggestund (motivasjon).
Mål: Eleven skal bli kjent med sannsynlighet og øve på bruk av formler i Excel.
Tidsbruk: Del 1; ca. 30 min. Del 2; ca. 45 min
Forberedelse: Formlene bør være tilgjengelig digitalt. Du trenger terninger med taktil merking, eventuelt må en annen elev på gruppa registrere resultatet.
DEL 1
Oppgave: Trill en terning hundre ganger og noter ned hvor mange 1-ere, 2-ere osv. du får. I grupper kan man dele opp og kaste noen ganger hver samtidig for så å sette sammen resultatene.
Før resultatene opp i en tabell i Excel og lag søylediagram.
Drøfting: Ble resultatet slik de hadde tenkt? Hvorfor? Hvorfor ikke?
DEL 2 Simulere terningkast i Excel.
Simulering av terningkast i Excel gjøres med formel: «=TILFELDIGMELLOM(1;6)», når cellen er markert kan man ta tak i den å dra nedover for å kopiere formelen til mange celler. Dette fungerer ikke uten mus, da kan man kopiere og lime inn med ctrl+D.
Forsøk å kaste mange hundre ganger. Ja kanskje tusenvis av ganger (Hvis elevene synes det er gøy).
For å få Excel til å telle opp antall enere, toere osv. Bruker du formel: «=ANTALL.HVIS(A1:A500;1)» for enere og bytt ut 1 med 2 for toere osv. Tabellen kan se slik ut:
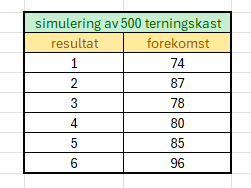
Med formler: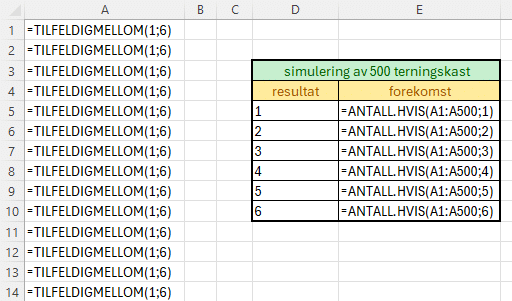
Du lager søylediagram ved å markere tabellen. Søylediagrammet vil endre seg hvis du endrer tallmengden tabellen henter resultatet fra. Med hurtigtaster markerer du tabell med shift+pil, og lager diagram med ctrl+q, så D.
Drøfting: Hvordan blir resultatet nå? (Jo flere kast, desto likere høyde på søylene)
Her kan man også snakke om store talls lov.
Mål: Få praktisk erfaring med kombinatorikk
Tidsbruk: ca. 30 min
Forberedelse: Lag gruppe med 4 eller 5 stoler på hver.
Gjennomføring: Oppgave: 4 eller 5 elever er på gruppe. Elevene går ut, og så kommer en og en elev inn og setter seg på en av stolene som tilhører gruppen.
Tilrettelegging: Det kan være lurt om punktskriftbrukeren får være den som setter seg først av gruppemedlemmene. Så slipper eleven å lete og kjenne på stoler hvor det sitter medelever.
Drøfting: Hvor mange plasser hadde hver å velge mellom. På hvor mange ulike måter kan de plassere seg?
Mål: Praktisk erfaring med modellering og arbeid med lineære funksjoner
Tidsbruk: ca. 60 min
Elevene samarbeider i grupper på to eller tre. Klassen går ut og vi måler opp en lengde på 10 eller 20 m. Elevene velger selv hvordan de vil bevege seg den lengden. Eks. Hoppe, hinke, gå baklengs, løpe. En elev tar tiden mens den andre beveger seg.
Vi går inn i klassen igjen og regner ut farten. Vi lager koordinatsystem der x-aksen er tid og y-aksen er avstand. Hver graf starter i origo og hver graf får et punkt med en y-verdi på 10 m (eller 20 m).
Oppgave: Lag din egen graf. Hva er gjennomsnittsfarten? Kan du finne funksjonsuttrykket?
Drøfting: Hvordan hadde denne grafen kunne utviklet seg hvis lengden økte veldig mye?
Gir grafen et reelt bilde? Er farten den samme hele veien?
Hentet fra TouchingMaths-prosjektet
Mål: Få en innføring i algoritmisk tenkning.
Tidsbruk: fra 30 min
Med ulike instrumenter, kan man «programmere» en melodi eller en rytme. I eksempelet bruker vi Boomwhackers, men andre instrumenter kan brukes.
Forberedelse: merk hvert Boomwhacker-rør taktilt med et tall eller en bokstav-forkortelse.
Lag en melodi ved å slå på ulike Boomwhacker-rør i en bestemt rekkefølge. Skriv en kode for melodien ved å bruke bokstav-forkortelsen til hvert rør. Jobb i par, og lag en kode for en melodi et annet par skal spille. Hvis en bit av koden skal gjentas, skriv for eksempel gjenta 3().
Med bokstavforkortelsene r (rød), l (lilla), b (blå), g (grønn), gu (gul) og o (oransje), kan man for eksempel lage koden
rrgu gjenta 2(bbgu) rrgu
rrgu gjenta 3(bbgu) rrgu
Hentet fra TouchingMaths-prosjektet
Mål: Få en innføring i algoritmisk tenkning
Tidsbruk: fra 45 min
Forberedelse: I denne aktiviteten kan elevene bruke lapper eller brikker med tekst eller punktskrift. Skriv «danse-instrukser» og kode-begreper på lappene/brikkene, som hopp, klapp, venstre, høyre, fremover, bakover, snu, hvis (if), mens (while), 90 grader, 180 grader, osv. Få gjerne hjelp av elevene til flere instrukser.
Å lage en dans kan sammenlignes med å lage en algoritme for programmering. Vi planlegger hva vi skal gjøre, når vi skal gjøre det, hvor fort, og hvor mange ganger vi skal gjøre et trinn. Så kan vi gjennomføre planen, og vurdere om vi skal gjøre noen endringer for å forbedre dansen.
La elevene jobbe sammen i par eller grupper for å lage en dans med lappene/brikkene, eller skriftlig i et tekstdokument. Elevene kan prøve dansen til andre par/grupper i klassen.
Mål: Enkelteleven får erfaring med å bruke sine matematiske ferdigheter til problemløsing
Tidsbruk: ca. 60 min
Oppgave: Kvadrat inni kvadrat. Elevene jobber i par og bruker Geobrett med strikk.
Lag et kvadrat der sidene er 8. (6+2) inni dette kvadratet lager du et kvadrat med sidene 4. (6-2).
Hvordan kan dere regne arealet mellom de to kvadratene?
Utvidelse: Kan dere endre størrelsen på kvadratene og bruke samme metode?
Kan dere finne en generell regel for hvilke som gjelder?
Kan dere lage et bokstavuttrykk der lengdene beskrives med
a +b og a -b?
Mål: Praktisk erfaring med begreper innen personlig økonomi og prosentregning
Tidsbruk: fra 60 min
Ta med klassen og gå på nærmeste butikk/senter (eller finne tilbud på nett).
De samarbeider to eller tre. Let etter det dere mener er gode tilbud. Bli enig om tre tilbud dere vil ta med tilbake til klassen.
I klasserommet. Hver gruppe presentere ett eller to tilbud de mener er gode, med begrunnelse.
Tilrettelegging: Her der det nødvendig med synstolkning i samarbeidet. Tips: Eleven samarbeider med en/flere som hen er trygg på og medelever synstolker.
Drøfting: Hvorfor er et tilbud et godt tilbud? Er det mest penger i avslag? Er det størst prosentvis avslag? Er det et godt tilbud hvis varen er lite populær?
Avslutning: Klassen stemmer frem det de mener er det aller beste tilbudet.