Koordinatsystem, grafer og funksjoner

Her finner du informasjon om hvordan en elev som bruker punktskrift kan lære om koordinatsystemet og grafer, og tips til undervisningsmetoder og læringsmateriell.

Koordinatsystemer og grafer gir en rask visuell oversikt over et tallmateriale. Det er lett å se forskjellen på grafen og selve koordinatsystemet, og hvordan grafen utvikler seg.

For en elev som leser taktilt, er det ikke like lett å få oversikt over en figur. Eleven må utforske figuren bit for bit og lage et mentalt bilde. Det kan være krevende å skille de ulike delene av figuren og å få oversikt over grafens form.

• Koordinatsystemet
• Verditabell
• Grafer
• Digital graftegning
• Regresjonsanalyse
• Funksjonsdrøfting

Koordinatsystemet

Vi anbefaler at eleven blir godt kjent med det taktile koordinatsystemet før eleven senere skal arbeide med grafer og diagrammer.

Eleven må utforske og gjenkjenne akser, origo, rutenett, koordinater og punkter taktilt, og skille mellom ulike mønstre.

Forstå koordinatsystemet

En stegvis opplæring i koordinatsystemet kan være nyttig for mange elever. Start med et enkelt koordinatsystem med bare aksene, og legg til nye elementer etter hvert som eleven blir tryggere. De ulike stegene kan være:

• Steg 1: Utforske akser, origo og kvadranter.
• Steg 2: Bli kjent med enhetene og øve på å telle langs aksene.
• Steg 3: Introdusere rutenettlinjer. Øve på å skille disse fra aksene og følge dem.
• Steg 4: Tall langs aksene: Lese tallene og øve på å følge rutenettlinjene mellom aksene og tallene.

Vi anbefaler at elevene lærer seg kvadrantnumrene. Det kan hjelpe eleven med å lage et mentalt bilde av koordinatsystemet, og gjør det lettere å snakke med andre om det.

For de yngste elevene kan det være aktuelt å starte med kun 1. kvadrant:

Steg 1:	Steg 2:	Steg 3:	Steg 4:

For elever som skal jobbe med alle fire kvadranter:

Steg 1:	Steg 2:	Steg 3:	Steg 4:

Punkter i koordinatsystemet

Hvordan plotte punkter i koordinatsystemet

Hvis du bruker et taktilt koordinatsystem, bør det festes til en myk tavle (for eksempel korkplate) med nåler.

For å markere punktet (3, 5): Finn først 3 på x-aksen. Følg deretter rutenettlinjen parallelt med y-aksen og tell fem trinn. Sett en nål i dette punktet (3, 5).

Øvelse: La eleven markere punktet (3, -2).

Det er vanskelig å lese eller markere punkter som ikke ligger på en linje i rutenettet helt nøyaktig. Eleven kan markere punktet ved å sette nålen mellom to linjer.

Hvordan lese av koordinatene til et punkt

For å bestemme koordinatene til et punkt, må eleven følge rutenettlinjen fra punktet til begge aksene.

Marker et punkt i første kvadrant med en nål. Følg rutenettlinjen med en pekefinger fra punktet til x-aksen (og videre nedover til tallene) og les av x-verdien. Flytt deretter pekefingeren tilbake til nålen og følg linjen til y-aksen (og videre mot venstre til tallene) for å lese av y-verdien.

Tips: For å følge rutenettlinjene bør eleven bevege pekefingeren med en viss fart for å holde seg på riktig linje. Går det for sakte kan det føre til at eleven mister oversikt over hvilken linje han følger.

Justerbare akser

Dette koordinatsystemet består av en plate og to løse akser – én kort og én lang. En taktil figur legges på platen, og aksene plasseres oppå. Den korte aksen kan være enten x-aksen eller y-aksen, avhengig av hvordan platen orienteres. Vi kan lage ulike koordinatsystemer ved å flytte på aksene, ved å variere både størrelsen på de ulike kvadrantene og hvilke kvadranter som skal vises.

Verditabell

Verditabellen kan lages i tekstbehandlerprogram eller regneark. For bedre oversikt på leselisten, bør tabellen stilles opp slik at x- og y-verdiene står parvis på samme linje.

Eksempel: Lag verditabell til funksjonen f gitt ved f(x) =2x -1.

Med tekstbehandlingsprogram

Eleven kan stille opp verditabell uten tabelloppsett, men bruke to mellomrom for å skille kolonnene. Det er ikke nødvendig å justere kolonnene rett under hverandre.

x  y

0  -1

2  3

4  7

Med regneark

Skriv funksjonsverdiene i kolonne A og formel for å beregne funksjonsverdier i kolonne B. Her er fremgangsmåten for å lage verditabell for funksjonen f(x) =2x -1 for x-verdier mellom 0 og 10 med steg 1:

1. Skriv kolonneoverskrifter x i celle A1 og f(x) i celle B1
2. Skriv minste verdi for x, 0, i celle A2.
3. Skriv =A2 +1 i celle A3 og Enter (da brukes 1 som steg for x i tabellen)
4. Merk området A3 til A12: start i celle A3, hold Shift-tasten inne og trykk pil ned 9 ganger.
5. Fyll ut kolonnen ved å trykke Ctrl+D.
6. Skriv =2*A2 -1 i celle B2 og Enter for å beregne første funksjonsverdi
7. Merk området B2 til B12 (Shift+pil ned)
8. Fyll ut kolonnen for f(x) ved å trykke Ctrl+D

Grafer

La eleven bli kjent med grafens form først, uten koordinatsystem. Bruk en taktil tegning, Wikki Stix, 3D-modell eller lignende. Når eleven kjenner formen godt, blir det lettere å gjenkjenne den i et koordinatsystem senere.

Tilpass figuren til elevens taktile ferdigheter. Det kan være lurt å starte med å plassere grafen i et enkelt koordinatsystem uten rutenett og uten tall på aksene.

Gi en muntlig forklaring før eleven begynner å utforske grafen. Bruk matematiske ord fra undervisningen, som skjæringspunkt, topp- og bunnpunkt, vekstfart og symmetrilinje.

Dersom flere grafer skal være i samme koordinatsystem, bør eleven først bli kjent med grafene hver for seg. Start med et koordinatsystem uten rutenett. Legg til én og én graf. Den nye grafen kan først lages med Wikki Stix for å skille den ut fra de andre. Når eleven er blitt kjent med alle grafene, kan de studeres sammen. Eleven kan utforske hvordan grafene ligger i forhold til hverandre, og eventuelt hvor de krysser hverandre.

Etterpå kan grafene vises i et mer detaljert koordinatsystem med rutenett og tall langs aksene. Unngå å ha mer enn tre grafer i samme figur. Hvis grafene ligger for tett, blir det vanskelig å skille dem fra hverandre.

Husk at elever som bruker punktskrift ikke kan lese av punkter og verdier like nøyaktig som seende. Gi god støtte og forklaring underveis.

Lese taktile grafer

Eleven bør først bruke håndflatene til å kjenne over hele grafen for å få oversikt. Etterpå kan eleven bruke fingertuppene til å undersøke detaljer.

Det er lurt å gi eleven systematisk opplæring i å lese taktile grafer. En trinnvis strategi kan være til hjelp, for eksempel slik:

1. Sjekk at arket ligger riktig vei.
2. Les overskriften og se etter forklaringer (nøkkel/tegnforklaring).
3. Finn aksene og origo.
4. Finn ut hvilke kvadranter som vises.
5. Les tallene langs aksene og finn ut hvor mye hvert trinn representerer.
6. Utforsk grafen: hva slags type graf er det? Let etter viktige punkter, som for eksempel skjæringspunkt, toppunkt og bunnpunkt.

Si gjerne navnet på de ulike delene mens eleven kjenner på dem. Dette gir trygghet og hjelper eleven å forstå sammenhengen mellom elementene i koordinatsystemet.

Til slutt kan eleven beskrive grafen med egne ord.

Lage taktile grafer

Det finnes flere metoder for å la eleven lage egne taktile grafer. Å øve på å plotte punkter og skissere en graf kan bidra til bedre forståelse. Vær oppmerksom på at dette tar lang tid, og at eleven ikke kan plotte like nøyaktig som en seende. For å spare tid og energi bør antall oppgaver begrenses og eleven kan trenge hjelp underveis.

Elev og lærer kan jobbe sammen om å plotte punkter i koordinatsystemet. Eleven vil erfare hvordan grafen utvikler seg etter hvert som flere punkter kommer på plass. Det taktile koordinatsystemet bør plasseres på en korkplate eller liknende, og nåler kan brukes for å markere punktene. Wikki Stix kan brukes for å tegne grafen, og nålene kan fjernes til slutt så det er lettere å kjenne grafen.

I stedet for å regne ut mange koordinater, bør eleven lære å finne sentrale punkter ut fra funksjonsuttrykket og plotte disse. Det kan også bidra til å styrke forståelse av sammenheng mellom graf og funksjonsuttrykk.

Lineære funksjoner

• Merk skjæringspunktet med y-aksen.
• Tell enheter ved hjelp av stigningstallet. Eksempel: hvis stigningstallet er 2, tell ett trinn i x-retning fra et punkt på grafen. Tell deretter to trinn i y-retningen og marker dette punktet.
• Merk skjæringspunktet med x-aksen.

Andregradsfunksjoner

• Merk nullpunktene og skjæring med y-aksen.
• Merk topp eller bunnpunkt.
• Tegn inn symmetriaksen og speil punkter om denne.

Digital graftegning

I skolen er Geogebra et mye brukt verktøy for å tegne og utforske grafer digitalt. For en elev som bruker skjermleser og leselist, er Geogebra lite egnet. Eleven bør derfor bruke andre digitale verktøy.

Regneark og Statpeds Excel-modeller

Eleven kan bruke regneark med ferdige formler for ulike funksjoner. Da kan eleven skrive inn koeffisiententene i funksjonsuttrykket og få informasjon om grafen. Læreren kan lage slike regneark selv.

Statped har laget Excel-modeller for å utforske grafen til disse funksjonene:

I tillegg til å få informasjon om grafens egenskaper i regnearkene, kan elevene også skrive inn en verdi for x, og få tilhørende verdi for f(x). Tilsvarende kan eleven skrive inn verdi for f(x) og regnearket beregner x.

Regnearket gir også en verditabell for funksjonen, og eleven kan skrive inn ønsket definisjonsmengde (x_min og x_max).

I arkene er cellene låst, bortsett fra cellene der eleven skal fylle inn verdier. Eleven kan hoppe mellom disse ved å bruke tabulator-tasten.

Desmos

Desmos er et digitalt verktøy for å tegne grafer. Desmos ligner på graftegneren i GeoGebra, men fungerer bedre sammen med skjermlesere. I tillegg kan Desmos gi en lydversjon av grafen.

Eleven skriver inn et funksjonsuttrykk i formelfeltet, og grafen vises i grafvinduet.

Når Desmos brukes med skjermleser, kan eleven få informasjon om viktige punkter på grafen, som skjæringspunkter med akser og andre grafer. Ved å bruke piltastene kan eleven bevege seg langs grafen og få koordinatene for hvert punkt opplest. Det finnes også hurtigtaster for å finne skjæringspunkter og andre interessante punkter. Her finner du en oversikt over alle hurtigtastene i Desmos.

Kombiner gjerne lydversjon av grafen i Desmos med en taktil figur av grafen. La eleven studere den taktile figuren først og bli kjent med grafens egenskaper.

Desmos kan også vise tekst i punktskrift, men den viser en notasjon som ikke brukes i Norge (Unified English Braille (UEB) eller Nemeth-kode). Derfor anbefales det ikke å bruke denne funksjonen.

Eksempel y =2x +3

Skriv funksjonsuttrykket inn i formelfeltet. Skjermleseren kan lese opp uttrykket, men vær klar over at dette kan skille seg fra hvordan eleven er vant til å lese det.

Når funksjonen er skrevet inn:

1. Trykk Alt + t for å starte lydvisning (Audio Trace).
2. Trykk h for å høre grafen.
   Lyden går fra venstre til høyre. Lysere tone betyr høyere y-verdi. Negative y-verdier gir en skurrende lyd. Når grafen krysser x-aksen, endres klangen. Med stereo hodetelefoner vil lyden flytte seg fra venstre til høyre øre. Dette gir et godt inntrykk av hvordan grafen utvikler seg.
   Siden funksjonen y =2x +3 har en graf som stiger, vil lyden bli lysere etter som markøren beveger seg fra venstre mot høyre.  
3. Bruk piltaster for å gå stegvis langs grafen. Skjermleseren leser opp koordinatene og sier ifra hvis det er et skjæringspunkt eller topp-/bunnpunkt.
   For y =2x +3 er de interessante punktene skjæringspunktene med aksene. Tab eller Shift + Tab vil hoppe mellom interessante punkter.
4. Trykk Escape for å gå tilbake til formelfeltet og redigere uttrykket.

Du kan justere hastigheten på lydvisningen ved å trykke Alt + (1–5), der 1 er den langsomste og 5 er den raskeste.

Det kan være nyttig å lytte til grafen flere ganger, og sammenligne det som høres med den taktile figuren av grafen, spesielt for å forstå hvordan lyden forandrer seg i ulike deler av koordinatsystemet.

Regresjonsanalyse

Manuell kurvetilpasning

Eleven plotter noen av punktene ved å sette nåler i et taktilt koordinatsystem, gjerne i samarbeid med lærer. For å undersøke om det er en lineær funksjon kan eleven legge en linjal inntil punktene. For andre funksjoner bør eleven sammenlikne punktene med modeller av de ulike funksjonstypene.

Digital regresjonsanalyse

For å bruke GeoGebra til å gjøre en regresjonsanalyse, trenger eleven assistanse. Eleven kan bruke R-tallet til å vurdere hvilken modell som passer best til datasettet.

Regresjon i regneark

Statped har laget et regneark som kan brukes til regresjon (kommer snart).

Fremgangsmåte:

1. Legg inn x-verdiene i kolonne A, og de tilsvarende y-verdiene i kolonne B
2. Velg ønsket regresjonsfunksjon:
   Ctrl+L: Lineær regresjon
   Ctrl+E: Eksponensialregresjon
   Ctrl+Q: Andregradsregresjon
   Ctrl+T: Tredjegradsregresjon
   Ctrl+W: Logaritmisk regresjon
   Ctrl+R: Potensregresjon

Resultatet kommer like under listene. Eventuelle feilmeldinger kommer i celle C1.

Desmos

Eleven kan legge inn data (x- og y-verdier) i Desmos og velge regresjonsmodell. I grafvinduet vises regresjonsfunksjonen sammen med datapunktene. Ulike fremgangsmåter er beskrevet på desmos.com.

Et godt tips er å skrive x- og y-verdiene i Excel og kopiere dataene til Desmos.

Eksempel på fremgangsmåte i Desmos:

1. Merk og kopier tabell med x- og y-verdier og lim inn i formellinjen i Desmos. Et plott av punktene vil vises i grafvinduet.
2. Trykk Tab for å komme til neste formellinje. Skriv inn formel for ønsket regresjonsfunksjon:
   Lineær: y\1 ~ ax\1+b
   Eksponential: y\1 ~ a*b^x\1
   Andregrad: y\1 ~ ax\1^2 +bx\1 +c
   Logaritmisk: y\1 ~ a +b *ln(x\1)
   Potens: y\1 ~ a*x\1^b

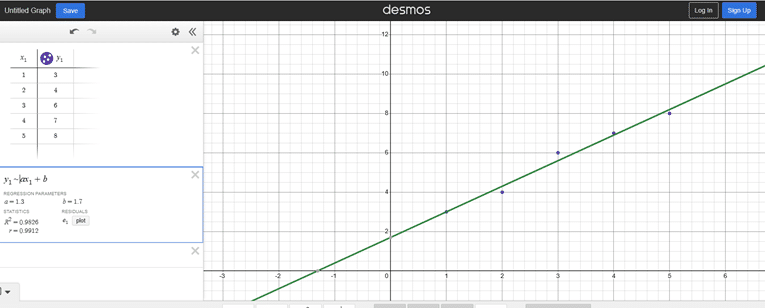
Vær oppmerksom på at eleven må bruke skjermleseren for å få ut informasjon om a, b, c og R-verdi. Det kan være vanskelig å få tilgang til all informasjonen gjennom skjermleseren. Et tips er å bruke kunstig intelligens til å tolke bildet. Eleven må da øve på å stille gode spørsmål for å få tilgang til ønsket informasjon. Hvis eleven bruker skjermleseren Jaws, kan den innebygde KI-funksjonen Jaws Picture Smart brukes.

Funksjonsdrøfting

For å utforske hvordan grafen utvikler seg i koordinatsystemet, bør eleven jobbe med taktile figurer av grafen. Bruk en linjal eller liknende for å studere hvordan helningen til tangenten endres langs grafen.

Veiled eleven til å beskrive muntlig hvordan helningen til tangenten endrer seg etter hvert som dere flytter den langs grafen. Bruk matematiske begreper. Fortsett eventuelt med å beskrive sammenhengen mellom stigningen til tangenten og formen til grafen akkurat der tangenten er.

Bruk av digitale verktøy

Vurder hele tiden hva  eleven skal lære når du skal avgjøre hvilke metoder og verktøy eleven skal bruke. Hva er hensikten med oppgaven og hva er læringsmålet? Mange av fremgangsmåtene kan være enkle å gjøre for en seende i Geogebra, men krevende å gjennomføre for eleven som bruker punktskrift. I mange tilfeller kan eleven få teknisk bistand til å bruke digitale verktøy som GeoGebra, og heller bruke tiden på å forstå og reflektere rundt det matematiske innholdet i oppgaven.

Fortegnsskjema

For å drøfte monotoniegenskaper kan eleven lage et fortegnsskjema.

• Positiv linje markeres med kolon: :::::
• Negativ linje markeres med komma: ,,,,,
• Nullpunkter markeres med at verdiene settes på de respektive linjene.

Eksemplet nedenfor viser fortegnskjema for den deriverte til f(x) =x^3 -6x^2 +9x

f’(x) =3x^2 -12x +9 =3(x -1)(x -3)

3  :::::::::::::::::::::::::::::::::::::::::::::::::::::

(x -1) ,,,,,,,,,,,,,,,,,1:::::::::::::::::::::::::::::::

(x -3) ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,3::::::::::::::

f'(x) :::::::::::::::::::1,,,,,,,,,,,,,,,,,3:::::::::::::